Discrete Homogenous Surfaces

Home Dedication Examples of Segments and Surfaces Games Angle Mathematics and Physics Angle Download User Manual Programmer Manual

While the surface shapes like cylinders and hemispheres seem intuitive, their logical organization needs some careful observation. As all boards have exactly one "square" or "unit" as a result of a move in any direction, for "unit"s in the middle of the board hardly anything interesting happens. All the boards differ based on what happens on the boundary. We divide our discussions in three parts: Boundary Conditions (what happens on individual boundary unit) Segments (what happens to one dimension)and Surfaces (what happens to a board) Boundary Conditions What all possibilities exist when a ball travelling rightwards hits on the wall? Possibility Name Picture The wall does not exist. The ball continues travel infinitely. This condition is nearly useless in games because at least one dimension becomes infinite. Infinite It is impossible to go further. The ball "sticks" to the wall till someone pushes it in other direction. This is the condition when you play "normal" chess. It is impossible to move a rook rightwards from the rightmost file. Geometric (like a segment in high school geometry) The wall is hard. The ball "bounces back". So for the same point, if the ball did not bounce earlier, it moves rightwards. If it did, from the same point, it moves *leftwards*. Again, if someone changes the direction of the ball, it moves rightwards and so on. This is similar to singing where you go to the highest note and then decrease in the pitch smoothly. This is also like climbing a mountain where in you reach the top contour and slowly return till you climb back up. This is also like traveling to the North Pole. Your latitude increases and then slowly decreases. Geodesic (like traveling through a geodesic pole) The wall is a part of circular tunnel. The ball "returns" at the origin. This is like running in a circle. Circular Segments - two conditions on one segment Interestingly, it is not possible to freely mix and match all the four boundary conditions. Intuitively circular boundary condition for the right hand side is valid only if the left side also "rolls over" to the right side. The other three conditions can freely be mixed and matched. For example, left hand could be a sticky wall and the right hand could be a bouncy wall. This gives rise to 10 possibilities for segments. As a convention, we have named each segment as left boundary condition - right boundary condition. Name Picture Infinite-Infinite Infinite-Geometric Infinite-Geodesic Geometric-Infinite Geometric-Geometric Geometric-Geodesic Geodesic-Infinite Geodesic-Geometric Geodesic-Geodesic Circular-Circular Surfaces - two Segments in each dimension Examples here are limited to finite surfaces. Images here are copied from http://images.google.com. These images may have applicable copyrights. 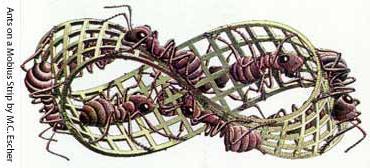Name Picture Horizontal Segment Vertical Segment "normal" flat board Geometric-Geometric Geometric-Geometric Vertical Cylinder Circular-Circular Geometric-Geometric Vertical Helical Cylinder Circular-Circular with the other dimension changes keeping difference between source and destination constant Geometric-Geometric Vertical Mobius Strip Circular-Circular Geometric-Geometric the other dimension changes keeping difference between source and destination constant Vertical "Regular" Sphere Circular-Circular Geodesic-Geodesic the other dimension changes keeping difference between source and destination constant Vertical "Regular" Hemisphere Circular-Circular Geometric-Geodesic the other dimension changes keeping difference between source and destination constant One of possible Vertical "Basketball" Spheres Circular-Circular Geodesic-Geodesic the other direction changes keeping modulo sum of source and destination constant "Doughnut" shape Circular-Circular Circular-Circular Klein bottle Circular-Circular Circular-Circular the other dimension changes keeping difference between source and destination constan